数学复数是数学中重要的概念之一,它在代数学、几何学、物理学等领域都有广泛的应用。本文将全面介绍数学复数的基本概念、运算规则以及应用,帮助读者深入理解与掌握数学复数。

一、复数的定义与表示方法
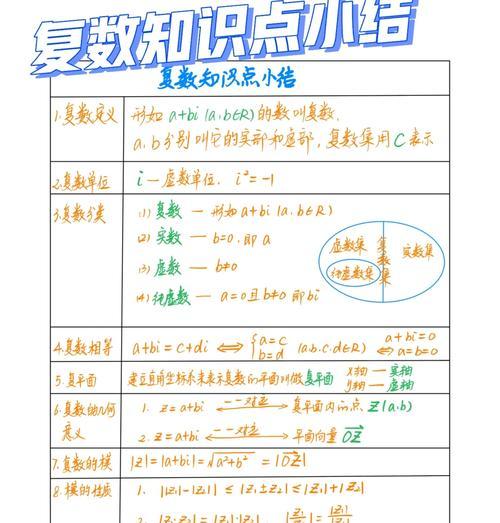
复数是由实部和虚部组成的,常用的表示方法有代数式、三角式和指数式,不同表示方法之间可以相互转换。
二、复数的基本运算法则
复数之间可以进行加减乘除等运算,其中加法和乘法满足交换律和结合律,而除法则需要特殊的处理。
三、复数的共轭与模
一个复数的共轭是将其虚部取负,模表示复数到原点的距离,共轭和模之间有一些重要的性质和关系。
四、复数在坐标平面上的表示
复数可以用来表示平面上的点,实部对应横坐标,虚部对应纵坐标,这种表示方式称为复平面。
五、复数的幂与根
复数的幂可以通过指数法则进行计算,复数的根有多个,其中最常见的是平方根和立方根。

六、复数与三角函数的关系
复数与三角函数之间存在着密切的关系,通过欧拉公式可以将复数表示为三角函数的形式。
七、复数的应用:电路分析
复数在电路分析中有广泛的应用,通过复数的运算可以方便地计算电路中的电流、电压和功率等参数。
八、复数的应用:信号处理
在信号处理领域中,复数被广泛应用于信号的频谱分析、滤波等处理过程中,为信号处理提供了强大的工具。
九、复数的应用:量子力学
在量子力学中,复数被用来描述波函数和量子态,通过复数的运算可以推导出丰富的物理性质和规律。
十、复数的应用:图像处理
图像处理中经常需要进行频域分析和滤波操作,而这些操作常常涉及到复数运算,通过复数处理可以实现图像的增强和修复。
十一、复数的应用:振动分析
在振动分析领域中,复数被广泛应用于计算振动信号的频谱、相位和幅值等参数,为振动分析提供了重要的工具。
十二、复数的应用:矩阵运算
复数在矩阵运算中也起着重要的作用,通过复数的运算可以方便地求解线性方程组和计算特征值等。
十三、复数的应用:微分方程
在微分方程中,复数常常用来表示解析解,通过复数的运算可以方便地求解一些特殊类型的微分方程。
十四、复数的应用:傅里叶级数
傅里叶级数中的频谱分析涉及到复数的运算,通过复数可以将一个周期信号分解成不同频率的正弦和余弦波。
十五、复数的应用:随机过程
在随机过程中,复数可以用来表示随机信号的特征和统计性质,通过复数运算可以方便地计算各种随机变量。
数学复数是一种重要且广泛应用的概念,在代数学、几何学、物理学等领域都具有重要意义。本文通过对复数的定义、运算规则和应用进行详细介绍,希望读者能够更加深入地理解与掌握数学复数的知识点。
标签: #数学复数

